Nested Polyhedral Frames
Glen Whitney and Alex Kontorovich are putting together a mathematical art expo visualizing Euler's formula for polyhedra, with polyhedra placed at their respective \( (v,e,f) \)-coordinates to form the plane \( v-e+f = 2 \) in 3-space. I thought we would look at another polyhedron construction method and hopefully end with something we can ship their way!
Setup
Our construction method for this activity is going to be running string through straws to create rigid frames. Here are some possible materials, but plenty of others will work:
You'll also want some scissors.
Depending on your background, you might already have a sense for which structures will be rigid and which will not. Our previous rigidity activity serves as a nice exploration of this concept. Here, the difference will be that we can cut the straws to whatever lengths we like, which will allow us to buttress shapes that would otherwise be nonrigid. Because of the algebra, spatial reasoning, and fine motor skills, I would recommend this for late middle school and up.
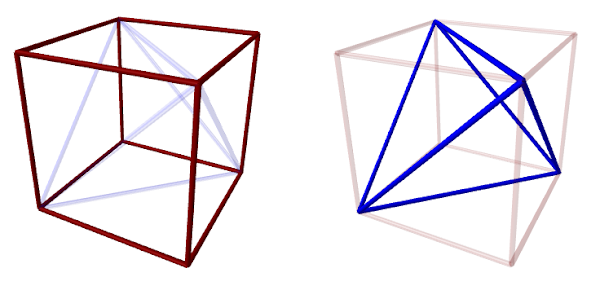
Example: Tetrahedron in Cube
If we choose four corners of a cube so that no two share an edge, connecting all pairs of these vertices with edges creates a tetrahedron inside the cube. Another way of thinking about this structure is starting with a tetrahedron and then growing a pyramid out of each face of just the right height so that the faces of each pyramid are flush with the faces of the neighboring pyramids.
To construct this, we'll need two lengths of straw. If we assume each of the edges of the cube has length \( x \), then the length of the edge of the tetrahedron must be given by \[ \sqrt{x^2 + x^2} = \sqrt{2} \cdot x \] For my scale, I'll choose \( x = 6 \, cm \) so that rounding to the nearest millimeter, my cube's side lengths are \( 6 \, cm \) and tetrahedron's side lengths are \( 8.5 \, cm \). While you don't have to color code, it certainly looks nicer:
We start by taking three of our tetrahedral edge straws, running string through them in series, and tying them off in a triangle. You want it tight enough to keep a triangular shape but not so tight that the straws press into each other and bend or warp:
We'll then create another triangle that shares an edge with our first triangle, creating a hinge of two triangles:
We then finish the tetrahedron by adding the sixth edge. I've done it by reinforcing both triangles that it's a part of with internal string loops. While you can get away with just looping through one triangle, the structure will be more sound if you reinforce every triangle with an internal loop.
We next begin building pyramids off of each of the tetrahedron's faces. We hinge a triangle from the structure by linking two cube edges to a cube edge:
We then finish the face-pyramid by adding another cube edge and reinforcing its triangles:
Similarly building a pyramid off of each of the tetrahedron's three other faces, we have our finished structure:
Example: Cube in Rhombic Dodecahedron
If we take a cube and grow a pyramid from each face until adjacent pyramidal faces are flush, we end up with a rhombic dodecahedron:
There might be ways to find these new lengths synthetically, but my default move is to coordinatize. If the cube's corners are \[ (1,1,1), (1,1,-1), (1,-1,1), (1,-1,-1), (-1,1,1), (-1,1,-1), (-1,-1,1), (-1,-1,-1), \] then, by symmetry, the six new vertices not on the cube must have coordinates \[ (a,0,0), (-a,0,0), (0,a,0), (0,-a,0), (0,0,a), (0,0,-a), \] for some \( a \). Since the apexes of adjacent pyramids must be collinear with the midpoint of their shared cube edge in order for their faces to be flush, we can take the three points \[ (a,0,0), (1,1,0), (0,a,0) \] as collinear, which forces \( a = 2 \). If a cube's edge has length \( 2 \) (the distance from \( (1,1,1) \) to \( (1,1,-1) \) ), then the length of a rhombic dodecahedral edge must be the distance from \( (1,1,1) \) to \( (2,0,0) \), i.e., \[ \sqrt{(2-1)^2 + (0-1)^2 + (0-1)^2} = \sqrt{3} \] Thus, if we choose a cube edge length of \( x \), our rhombic dodecahedron's edge length will be \( \frac{\sqrt{3}}{2} x \).
While this structure is rigid without a tetrahedron buttressing the cube, we'll go ahead and build the dodecahedron around the structure we made in the last example. Since we used \( x = 6 cm \) for our cube edge, we'll use \( 5.2 cm \) for our rhombic dodecahedron's edges:
Here is the figure after having one pyramid added:
Here is the final figure:
Initial Questions
- What other sorts of structures can be constructed in this way?
- What's a good way to go about finding a next structure to nest an existing structure within?
Explorations
Since many people know the Platonic solids, this is a great place to explore. We've seen what happens when we start with a tetrahedron or cube and extend them with pyramids so their faces are flush. Given that the cube and octahedron are dual, it might not surprise you to see that extending the octahedron in this way also results in a rhombic dodecahedron:
One way to think about this model is as polyhedron whose vertices are the union of all cube and octahedron vertices and whose edges are those that connect each cube vertex to its nearest octahedron vertices. Here is a model from straws and string using a longer edge length than we've used so far:
In this scheme, the ratio of side lengths for \[ tetrahedron \, : \, cube \, : \, rhombic \,\, dodecahedron \, : \, octahedron \] is \[ 2\sqrt{2} \,\, : \,\, 2 \,\, : \,\, \sqrt{3} \,\, : \,\, 2 \sqrt{2} \] or \[ \sqrt{2} \,\, : \,\, 1 \,\, : \,\, \frac{\sqrt{3}}{2} \,\, : \,\, \sqrt{2} \]
Similarly, the duality of the dodecahedron and icosahedron makes both of them give rise to the rhombic triacontahedron.
If we take the vertices of the dodecahedron to be \[ (-1,-1,-1),(-1,-1,1),(-1,1,-1),(-1,1,1),(1,-1,-1),(1,-1,1),(1,1,-1),(1,1,1) \] and \[ \left(\phi,\frac{1}{\phi},0\right),\left(\phi,-\frac{1}{\phi},0\right),\left(-\phi,\frac{1}{\phi},0\right),\left(-\phi,-\frac{1}{\phi},0\right), \left(0,\phi,\frac{1}{\phi}\right),\left(0,\phi,-\frac{1}{\phi}\right), \] \[ \left(0,-\phi,\frac{1}{\phi}\right),\left(0,-\phi,-\frac{1}{\phi}\right), \left(\frac{1}{\phi},0,\phi\right),\left(-\frac{1}{\phi},0,\phi\right),\left(\frac{1}{\phi},0,-\phi\right),\left(-\frac{1}{\phi},0,-\phi\right) \] for \[ \phi = \frac{1+\sqrt{5}}{2} \] and the vertices of the icosahedron to be \[ (1,\phi,0),(1,-\phi,0),(-1,\phi,0),(-1,-\phi,0), (0,1,\phi),(0,1,-\phi), \] \[ (0,-1,\phi),(0,-1,-\phi), (\phi,0,1),(\phi,0,-1),(-\phi,0,1),(-\phi,0,-1) \] then the ratios of edge lengths \[ dodecahedron \, : \, rhombic \,\, triacontahedron \, : \, icosahedron \] is \[ \sqrt{5} - 1 \,\, : \,\, \sqrt{\frac{5-\sqrt{5}}{2}} \,\, : \,\, 2 \] or \[ 1 \,\, : \,\, \frac{\sqrt{10+2\sqrt{5}}}{4} \,\, : \,\, \frac{1+\sqrt{5}}{2} \]
If we want to continue building on the model we made in the examples, we could try to grow a pyramid out of each face of the rhombic dodecahedron. Since the rhombi are no longer regular polygons, this will require two edge lengths. In our coordinate system, for these pyramids to be flush, the new vertices would need to be added at \[ \left(\frac{4}{3},\frac{4}{3},0\right),\left(\frac{4}{3},-\frac{4}{3},0\right),\left(-\frac{4}{3},\frac{4}{3},0\right),\left(-\frac{4}{3},-\frac{4}{3},0\right), \left(0,\frac{4}{3},\frac{4}{3}\right),\left(0,\frac{4}{3},-\frac{4}{3}\right), \] \[ \left(0,-\frac{4}{3},\frac{4}{3}\right),\left(0,-\frac{4}{3},-\frac{4}{3}\right), \left(\frac{4}{3},0,\frac{4}{3}\right),\left(\frac{4}{3},0,-\frac{4}{3}\right),\left(-\frac{4}{3},0,\frac{4}{3}\right),\left(-\frac{4}{3},0,-\frac{4}{3}\right) \] This gives a polyhedron with kites as faces known as a deltoidal icositetrahedron:
Here is a model I made a couple years ago that is now unfortunately falling apart:
Recalling that our edge ratio for \[ tetrahedron \, : \, cube \, : \, rhombic \,\, dodecahedron \] is \[ \sqrt{2} \,\, : \,\, 1 \,\, : \,\, \frac{\sqrt{3}}{2}, \] these two new edges are then \[ \frac{\sqrt{11}}{6} \qquad \textrm{ and } \qquad \frac{\sqrt{5}}{3}. \] for short and long, respectively.
Prisms and antiprisms are another pair of nice families to explore using this buttressing system.
Wrap-Up Questions
- Even though a rhombus isn't a regular polygon, there is still a clear center that the apex of a pyramid could sit above. Is there a nice way to grow a pyramid from a more irregular shape?
- Is there ever more than one "good" way to grow a structure according to our pyramids with flush faces convention?
Notes
Making these can be kind of tricky. It's a little gross, but you can mostly run string through straw by sucking it through. For some more delicate models, I will sometimes cut a straw along its length and use it as a sort of catch that can aid me in threading string through another straw. Since this requires a lot of patience and fine motor skills, I've tried to find other methods of connecting straws (pipe cleaner or paperclip vertex joints and putty, to name a few), but none have really given these models structural integrity. If anyone can suggest a simpler construction system on a comparable budget, I'd be very curious to hear about it!






















Comments
Post a Comment