Boring Conversations

Gord Hamilton's Kickstarter for The Infinite Pickle is very close to meeting its goal, so I thought today we'd look at a small corner of Boring Conversations, an activity from this collection that was presented this week at the Math Incubator workshop.

If you would like to support The Infinite Pickle, there is still time until Sunday, May 7th! Check it out here.

Setup

This activity can be run as a pencil-and-paper activity, but it would be more fun with a colorful manipulative. The downside of that is you would probably want enough colors that you would run into the ability of color-blind folks to easily distinguish them, so numeric labels would be appropriate. Here are some options in the spirit of Gord's version:

100 Wooden Meeples ($15, 10 colors)
128 Plastic Pawns ($12, 8 colors)
100 Plastic Peeples ($16, 10 colors)

Here are some worksheets with spaces to place the meeples.

While The Infinite Pickle has a lot of different versions of this problem to explore, we'll focus on this particular formulation:

A group of people will sit around a circular table for dinner but don't enjoy talking to the same person twice. How many nights in a row can they eat together so that no two people are seated next to each other for more than one meal? What should the table seating look like for each night?

Example

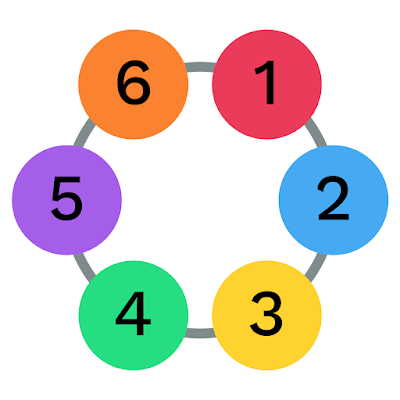
If there are 6 people, here is a way they can have dinner two nights in a row:

Initial Questions

How many nights can 4 people have dinner together?
How many nights can 5 people have dinner together?
We've seen that 6 people can have dinner together two nights in a row. Is it possible they could dine together a third night? Why or why not?
How do things work with 7 people? 8? 9? 10?
Is there a way to predict the number of nights possible just based on the number of diners? How can you determine the seating arrangements?

Explorations

At each meal, a diner has two neighbors, so each night eliminates two more neighbors for the next night. Since a diner also cannot be their own neighbor, this means that the number of nights we could expect is at most half the number of other diners, or
\[ \frac{n-1}{2} \]
Since it needs to be an integer, we could round down to get
\[ \left\lfloor \frac{n-1}{2} \right\rfloor \]
which is $ (n-1)/2 $ when $ n $ is odd and $(n-2)/2$ when $ n $ is even. Students that don't deal in division might be able to articulate this in terms of repeated subtraction. For example, if there are 8 diners, then
\[ 8 - 1 - 2 - 2 - 2 = 1 \]
and
\[ 8 - 1 - 2 - 2 - 2 - 2 = -1 \]
Suggests the largest number of dinners we can expect is 3, since a fourth dinner would require one more diner to provide a new neighbor.
Sometimes there are nice ways to generate other seating arrangements by modifying others. For example, consider the arrangement below of 12 diners.

You can take the even-numbered diners and rotate them in two ways so no two diners are neighbors twice:

We're hoping to get $\lfloor (12-1)/2 \rfloor = 5$ dinners, and this provides three. Maybe there are two more that are compatible with these three?

You might be able to think of some other ways to move some diners relative to others via rotations, reflections, or other symmetries.
One slightly more arithmetic way to plan out table settings works especially well when $n$ is prime. For example, if we have $n = 7$ people, we can arrange vertices labeled $1-7$ in a circle. Choosing a value $m$ relatively prime to $7$, we can connect vertex $1$ to vertex $1+m$, then $1+m$ to $1+2m$, and so on, interpreting $1+km$ as $1+km \mod n$ when the values get too large. Below are the arrangements we see for $m = 1, 2, 3$ (note: $m = 4, 5, 6$ generate these same figures):

In order to create the table arrangements for these, start at 1 and recite the numbers you pass through while following the lines until you return to 1. These are the arrangements we get from each of the diagrams above:

The diagrams are not necessary and students often discover these sorts of patterns by focusing on odds and evens, skipping every other number, or something similar.

When $n$ is not prime, we can still generate some arrangements in this way, but the arrangements will not achieve the expected upper bound. For example, for $n = 9$, the values $m = 1, 2, 4$ generate the diagrams

and seating arrangements

Since a fourth arrangement would require diners 1, 4, and 7 each somehow be neighbors with the other two around a 9-person table, these three seating arrangements cannot be extended to a fourth. However, it is possible to have four compatible seating arrangements!
One way to interpret the solutions for $n = 7$ is graph theoretically. If we combine all three diagrams, we get an edge-coloring of the complete graph on 7 vertices, $K_7$:

We'll discuss some strategies that revolve around this interpretation. Though it's unlikely students will stumble upon them, they illustrate that the upper bound discussed above is always attainable and provide a way to create the seating arrangements.
- For an odd number of diners, the problem of table settings can be reframed in terms of taking $K_n$ and partitioning its edges into disjoint Hamiltonian cycles -- i.e., loops passing through every vertex exactly once. This is known as a Hamiltonian decomposition. It's a classical result that this is always possible for odd complete graphs, but it's easiest to see this with a different representation of the graph. For 7 vertices, the way we'll think about it is by first placing 6 vertices in a ring. We will then create a path that connects pairs of vertices across from one another before zig-zagging down to the next level:
  
  We'll eventually place the 7th vertex and connect it to the two ends like this:
  
  Before placing the final vertex, we'll take the zig-zag path and recreate every rotation of it:
  
  Adding in the 7th vertex and connecting it to the ends of all zig-zag paths gives us the desired Hamiltonian decomposition:
  
  Here are the resulting seating arrangements from tracing the cycles:
  
  Here is the analogous Hamiltonian decomposition of $K_9$ and the four seating arrangements it suggests:
- For an even number of diners, the best we could hope for is that each diner is eventually seated next to everyone else except for one other diner. In graph theoretic language, this is asking for a Hamiltonian decomposition of $K_n$ after first removing a perfect matching (i.e., a set of edges that covers each vertex exactly once). Since any perfect matching is the same up to relabeling the vertices, let's choose an easy one to work with visually. For $K_8$, we'll arrange the vertices into a regular heptagon with a single vertex in the center. One nice perfect matching is made by connecting the middle vertex to an outer vertex and then creating all chords perpendicular:
  
  There are seven of these perfect matchings that are all rotations of one another, and they give a decomposition of $K_7$ into perfect matchings:
  If we take one of our perfect matchings and its nearest rotation, the two combine to give a Hamiltonian cycle:
  
  If we combine this Hamiltonian cycle with two of its rotations, we get a Hamiltonian decomposition of $K_8$ after deleting the seventh perfect matching (added in green on the right):
  
  Tracing each of the Hamilton cycles in the leftmost image above results in the three seating arrangements below:
  
  Here is the analogous Hamiltonian decomposition of $K_{10}$ minus a perfect matching and the four seating arrangements it suggests:
We've seen that we can always come up with a Hamiltonian decomposition for $K_n$ when $n$ is odd or $K_n$ minus a perfect matching when $n$ is even, so this shows we can always achieve our upper bound of
\[ \left\lfloor \frac{n-1}{2} \right\rfloor \]
compatible seating arrangements for $n$ people.

Wrap-Up Questions

What were some strategies for creating seating arrangements?
Were there any strategies that worked particularly well? What made them so nice?
Were some numbers of people easier to work with than others? Why was that the case?

Extensions

For many, many more extensions, check out this online copy of The Infinite Pickle. Here are a couple extensions that more closely relate to the variant we've looked at today:

The specific variant we've looked at today is a special case of the Oberwolfach problem:

Suppose you have $n$ people and $k$ tables with sizes $m_1, m_2, ..., m_k$ that seat $m_1 + m_2 + ... + m_k = n$ people, total. How many consecutive nights can people be seated for dinner so that no two people are neighbors twice?

The upper bound is again $(n-1)/2$, but it is not always achievable, so the heart of the Oberwolfach problem is deciding for which table sizes it can be achieved. (Our special case is $k = 1$, with $m_1 = n$, for which we've seen the upper bound is always achievable.)
A fun idea Gord introduces is the idea of clones. Being seated next to someone is equivalent to being seated next to their clone, so you can only sit next to any version of a person for one dinner. However, you and your clones can sit next to as many copies of them and their clones as you like for that one meal. You and your clones may be seated next to each other for at most one dinner. An easing into this problem might be to consider guests 1 through $n$ as usual but include a clone of guest 1 as the $(n+1)$st guest. How does this change things from our explorations above?

This post was sponsored by the Julia Robinson Mathematics Festival

Search This Blog

math them