Magical Corner Sums

As our community math circle prepares to run Magic Flowers, I've been looking at extensions and related problems. Here we'll look at a series of puzzles that also require certain sums to be the same.

Setup

Even though the puzzles we'll look at will be 2D, they were inspired by this old chestnut:

Is it possible to label the corners of a cube with the numbers 1-8 so that the four corners of each face give the same sum?

This is a great toy problem for a session. It turns out there are three distinct solutions up to rotation and reflection, but finding them and proving that those are all of them provides an arc with some nice discoveries.

Today we'll focus mostly on squares arranged into various polyomino configurations and try to label them so each square has the same corner-sum. Here are a couple puzzles to get the ball rolling:

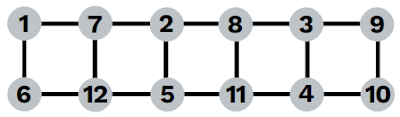
Example 1

Place the numbers 1-8 in the eight vertices so that the four corners of each square have the same sum:

Example 2

Place the numbers 1-8 in the eight vertices so that the four corners of each square have the same sum:

I've put together some worksheets. These puzzles are tricky and I have not solved all them, so be warned that some may be impossible! We'll discuss some of the solvable families below.

Initial Questions

• What do solutions to the example puzzles look like?

• What are the magic numbers for your solutions? (i.e., what are the corner sums?)

• Is there more than one way to solve these puzzles? If so, what magic numbers can you find?

• Can your solution methods be used on other puzzles?

Explorations

• An easy solution to the the family of rectangles that the first example belongs to is to place the numbers \(1-n\) counterclockwise, starting with the upper left position. This gives each vertical edge the same sum:

  

  These puzzles also offer a nice opportunity to observe that if two squares share an edge, then the edges that they don't share must have the same sum in order for the corners of each square to have the same sum. This gives a way to make other solutions by creating pairings into two sums, as in the solution below with edge sums alternating between 7 and 19:

  

  It's interesting to note that both of these solutions above have the same magic number, 26. This does not always need to be the case, as illustrated by these solutions for smaller rectangles with magic numbers 12, 13, 14, 15, and 16:

  

  If the number of vertices \(n\) is divisible by \(4\), then the vertical edges pair up to form \(n/4\) squares, with \(n/4-1\) squares between them. The magic number must then be the sum of the numbers \(1, 2, ..., n\), divided by \(n/4\), i.e.,

  \[ m = \frac{1 + 2 + ... + n}{n/4} = \left(\frac{4}{n}\right)\left(\frac{n(n+1)}{2}\right) = 2(n+1). \]

  In that case, the magic number is the same for any solution. If \(n\) is not divisible by \(4\) (but still even), we can't do this pairing of edges into squares, since one edge will be left over, so there is a possibility of several distinct magic numbers. So while there are several solutions to the first example with 1-8, they all have magic number 18.

• Shapes that feature a "crossroads" require two compatible rectangles of alternating edge sums. Here we have a solution to the example that features alternating 8,8 edges crossing alternating 12,4 edges for a magic number of 16:

  

  You can find solutions to this puzzle with magic numbers 15, 16, 17, 19, 20, and 21, but not 18. I'm not sure if there is a nice way to go about constructing these solutions or if one of the constructions lends itself to a general construction for ell shapes or zig-zag shapes. In some cases we can use a solution to one crossroads shape to get another by taking edges from one end of a road and attaching them to the other. For example, a solution to the T pentomino can be used to find a solution to the X pentomino or vice versa.

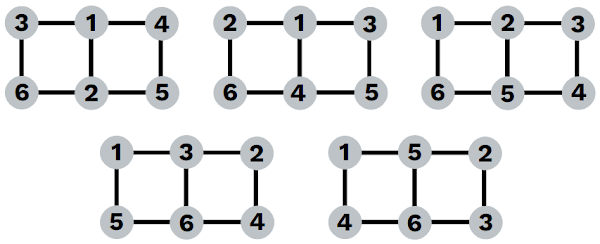
• Labeling the \(2 \times 2\) square below is a cute problem that is related to a few other problems.

  

  If you can find a solution to this puzzle with 1-9 using 9 in a corner, then removing that corner gives a solution to the previous ell-shaped puzzle. Another puzzle this relates to is the perimeter magic square below.

  

  If you can find a way to fill the square perimeter with 1-8 so that each edge has the same sum, then we can turn that into a solution to the corner sum puzzle as follows. Place your perimeter magic square solution into the border of the corner-sum puzzle but rotated so that corners are placed in edges and edges in corners. Then place 9 in the middle:

  

  It is possible to fill out the grid with 1-9 so that all four squares' corners sum to any of 16-24.

  If we were to label the vertices of a \(3 \times 3\) grid of squares with 1-16, if we focus on the four corner squares, we see that the magic number would have to be

  \[ \frac{1+2+3+...+16}{4} = 34. \]

  Here is one such solution:

  

• A standard trick for using one solution to come up with another in puzzles like this is to create a complementary solution in the following way. If the numbers \(1-n\) were used, relabel each vertex with \((n+1)-k\), where \(k\) is the current label. In this way, if the sum of a square's corners had been \(m = k_1 + k_2 + k_3 + k_4\), that square in the new solution has corner sum

  \[ ((n+1)-k_1) + ((n+1)-k_2) + ((n+1)-k_3) + ((n+1)-k_4) = 4(n+1) - m. \]

  Thus, we turn a solution with magic number \(m\) into a new solution with magic number \(4(n+1) - m\).

• If you're still chewing on the cube problem, here are the three solutions:

  

  (If you want to see why these are the only solutions, focus on the numbers 1 and 2 and where they could possibly be relative to one another!)

Wrap-Up Questions

• Are there any nice systems for finding magic corner labelings?

• Are there any families (like the \(1 \times n\) rectangles) where you made some interesting discoveries?

Extensions

• We have mostly explored puzzles based on patterns made from squares in a grid, but other shapes might prove interesting.

  • What about hexagons?

  • What about rhombi?

  • Triangles on their own are not great, since two adjacent triangles require their unshared vertices to have the same label, but what about configurations of triangles and quadrilaterals?

• Instead of labeling the vertices, we could label the edges.

• Can we label the 12 edges of a cube with 1-12 so that all edge-sums of the faces are the same? If so, how many ways are there to do so?

• How do our other puzzles change if we are instead labeling edges instead of vertices? Do the \(1 \times n\) rectangles still have a nice solution?

This post was sponsored by the Julia Robinson Mathematics Festival