Instant Insanity

Today we'll look at an old puzzle that has gone by many names over the centuries, my favorite name being "The Great Tantalizer." The most popular recent iteration was Parker Brothers' "Instant Insanity," so that's what most people call it. We'll look at some variations that let students explore how this puzzle might be easy (or at least easier), hard, or impossible.

Setup

While each commercial version of this puzzle had specific blocks, we'll be using a custom set that you'll want to make on your own. I've created some paper nets that can be used to build them, if you want an accompanying arts and crafts activity. For greater durability, you can print them on cardstock. I've tried to choose a palette that plays nicely with color-blindness, but please let me know if there are issues!

Otherwise, you can take the nets and translate them into your medium of choice. I've run a similar activity in the past using wooden cubes and markers or stickers. I've also done this using things like Polydrons and Geometiles. I found the lack of friction between cubes tough to work around, but they were nice for allowing students to design their own cubes. Since I'll give instructions in terms of cube numbers, I've pipped my cubes so you can easily tell cube \(2\) from cube \(4\), for example. You may want to similarly label your cubes with numbers, letters, shapes, or otherwise.

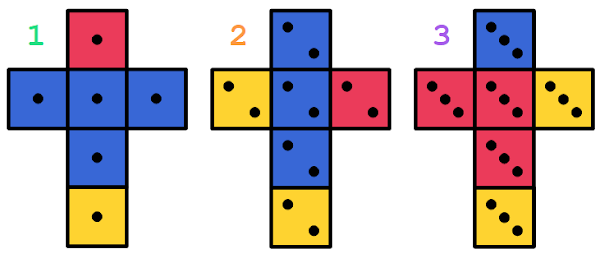
The premise of this puzzle is simple. To start, you will have three cubes where each face can have one of three different colors (red, yellow, blue). Your job is to stack them into a tower so that along each of the four faces of the tower, all three colors are visible -- i.e., each face will have three squares, one square of each color, as in the image below.

Challenges

The cube nets I've provided come in two sets: the first four (pages 3.1-3.2) and the last five (pages 4.1-4.3). If you accidentally mix them up, you can tell them apart since each of the cubes in the first set features three colors (red, yellow, blue) while each in the second set features four colors (red, yellow, blue, turquoise), so the turquoise allows for easy sorting.

For the following challenges, use the first set of cubes (the ones with red, yellow, and blue but no turquoise). Feel free to skip around, since some of these will likely be easier than others!

Set aside cube \(4\) and try solving the puzzle with cubes \(1, 2, 3\).
Set aside cube \(3\) and try solving the puzzle with cubes \(1, 2, 4\).
Set aside cube \(2\) and try solving the puzzle with cubes \(1, 3, 4\).
Set aside cube \(1\) and try solving the puzzle with cubes \(2, 3, 4\).

For the following challenges, use the second set of cubes (the ones with red, yellow, blue, and turquoise). This time there are four colors, so you will be building a tower with four cubes so that each face has all four colors on display. Feel free to skip around. Some of the puzzles are easier than others, but at least one of these puzzles is actually impossible!

Set aside cube \(5\) and try solving the puzzle with cubes \(1, 2, 3, 4\).
Set aside cube \(4\) and try solving the puzzle with cubes \(1, 2, 3, 5\).
Set aside cube \(3\) and try solving the puzzle with cubes \(1, 2, 4, 5\).
Set aside cube \(2\) and try solving the puzzle with cubes \(1, 3, 4, 5\).
Set aside cube \(1\) and try solving the puzzle with cubes \(2, 3, 4, 5\).

As you work through the challenges above, try to devise a strategy for solving them. How can you tell when a puzzle is impossible?

Notes

The classic solution to Instant Insanity uses graph theory. The idea is as follows, using cubes \(1,2,3\) from our first set.
- Draw vertices corresponding to the three colors (red, blue, and yellow).
- On each cube, if two colors are on opposite faces, draw an edge between those two colors on the graph, labeling it with the number of the cube. If a color is opposite itself, draw a loop from the vertex to itself. If one color is opposite another more than once, then draw a corresponding number of edges. Below is the graph we end up with:
- Next, we search our graph for subgraphs that feature each cube number on exactly one edge and where every vertex has degree \(2\). We want to find a pair of such subgraphs that do not share any edges. Below is an example of such a pair:
  
  We only need one pair, but here's another such pair just to showcase another configuration:
- Next, we use our pair of subgraphs to orient our blocks before stacking them. Taking the left subgraph to indicate north-south opposite pairs and the subgraph on the right to indicate east-west, we use the \(1\) edges to orient cube \(1\) and so on. Since the tops and bottoms do not matter, we use those to flip the cube upside down, if needed, to orient each axis correctly. The subgraphs actually give us a slick way to accomplish this orientation. If you orient blue east on one cube, for example, because blue has degree \(2\) in that right subgraph, you will then know which cube must have blue oriented west based on what the other edge is adjacent to blue. After all three cubes are oriented correctly, stack them.
  
  Here is one pair of subgraphs and the solution it induces:
  
  Here is our other pair of subgraphs and the solution it induces:
If a puzzle has a solution, it actually has a large family of related solutions. For example, the order that we stack the cubes in doesn't matter, since if all four colors appear on all sides, they will still all appear on each side after reordering. There are the usual symmetries of rotation and flipping the tower upside down. There are \(24\) rotations of a cube and \(n!\) ways to stack \(n\) of them, giving us \(24^n \cdot n!\) ways to stack \n\) cubes if we care which side faces us. For a given stack of \(n\), there are \(n!\) ways to reorder the cubes in the stack, \(4\) rotations, and \(2\) orientations (top-up vs bottom-up), giving \(8 \cdot n!\) equivalent stacks, as far as a solution is concerned. This gives
\[ \frac{24^n \cdot n!}{8 \cdot n!} = 3(24)^{n-1} \]
essentially distinct stacking configurations, meaning that if you were to randomly stack \(3\) cubes with three colors, if the puzzle has a unique solution (up to symmetry), you would have a
\[ \frac{1}{3(24)^{3-1}} = \frac{1}{1728} \]
chance of stumbling upon a solution each time you randomly put the three cubes together. Similarly, for four cubes with four colors, that probability is
\[ \frac{1}{3(24)^{4-1}} = \frac{1}{41472} \]

The cube sets I've created don't all have unique solutions up to symmetry, however. For example, we've seen that cubes \(1,2,3\) from the first, three-color set have at least two characteristically different solutions. We can count different solution types by creating the graphs and counting compatible subgraph pairs, which is what I've done. Below is some data on the puzzles you can get with each cube set, the number of different solutions (up to symmetry), and the probability of randomly finding a solution each time you randomly stack the cubes.

First set (red, yellow, blue):

Cubes	Solutions	Probability
\(1,2,3\)	\(4\)	\(1/432 \approx 0.231\%\)
\(1,2,4\)	\(1\)	\(1/1728 \approx 0.058\%\)
\(1,3,4\)	\(8\)	\(1/216 \approx 0.463\%\)
\(2,3,4\)	\(6\)	\(1/288 \approx 0.347\%\)

Second set (red, yellow, blue, turquoise):

Cubes	Solutions	Probability
\(1,2,3,4\)	\(2\)	\(1/20736 \approx 0.0048\%\)
\(1,2,3,5\)	\(0\)	\(0\)
\(1,2,4,5\)	\(11\)	\(11/41472 \approx 0.0265\%\)
\(1,3,4,5\)	\(1\)	\(1/41472 \approx 0.0024\%\)
\(2,3,4,5\)	\(7\)	\(7/41472 \approx 0.0169\%\)

Extra Challenges

Students might like designing their own set of cubes. Can they put together a set of cubes that has a solution? How about in a way that it isn't too easy to solve? Friends can design their own sets, swap, and try to solve each other's puzzles.
This puzzle generalizes to more colors. My cube sets have featured every color on every cube, which sets a color limit of \(6\), but that's not strictly necessary. Here is a set of \(6\) cubes with \(5\) colors (R,Y,G,B,V) that students might like investigating, given in terms of opposite face pairings:
- Cube \(1\): BV, RG, YG
- Cube \(2\): RV, GB, YV
- Cube \(3\): RV, GB, YB
- Cube \(4\): GV, YV, RB
- Cube \(5\): RY, RV, GB
- Cube \(6\): YB, GV, RV
The six puzzles here have \(0,1,1,2,3,4\) characteristically different solutions, but I'll let you decide which are which!

I think the most interesting thing about increasing the number of colors is finding out what the new types of subgraphs can look like, which can of course be explored as its own problem.
The Demaines et al. have written a paper discussing different variations on the puzzle, including a version with prisms instead of cubes!

This post was sponsored by the Julia Robinson Mathematics Festival

Search This Blog

math them