Pancake Flipping

Today we'll look at a puzzle set based on a classic problem about flipping pancakes.

Setup

If I've run this activity in the past, it was likely as a pen-and-paper exploration for older students. One possible way to run it is with Cuisenaire rods, which is what our graphics will resemble. Here are some options for those:

• Small class pack (155 for $30)

• Big class pack (444 for $70)

If you happen to have one, a Tower of Hanoi set is a nice manipulative. If looking at other stacking toys, the danger is that the column the rings stack around might actually be a cone instead of a cylinder, which prohibits stacking in all the necessary configurations.

The premise of this activity is there is a stack of pancakes of various sizes (e.g., radii \(1, 2, 3, ..., n\)) but in some jumbled order. Your job is to reorder them so that the pancakes increase in size from the top of the stack to the bottom. However, the only tool you have is a spatula that you can insert somewhere in the stack under the top \(k\) pancakes, lift those \(k\) pancakes off the top of the stack, and flip this stack of \(k\) pancakes upside down, replacing it on top of the stack.

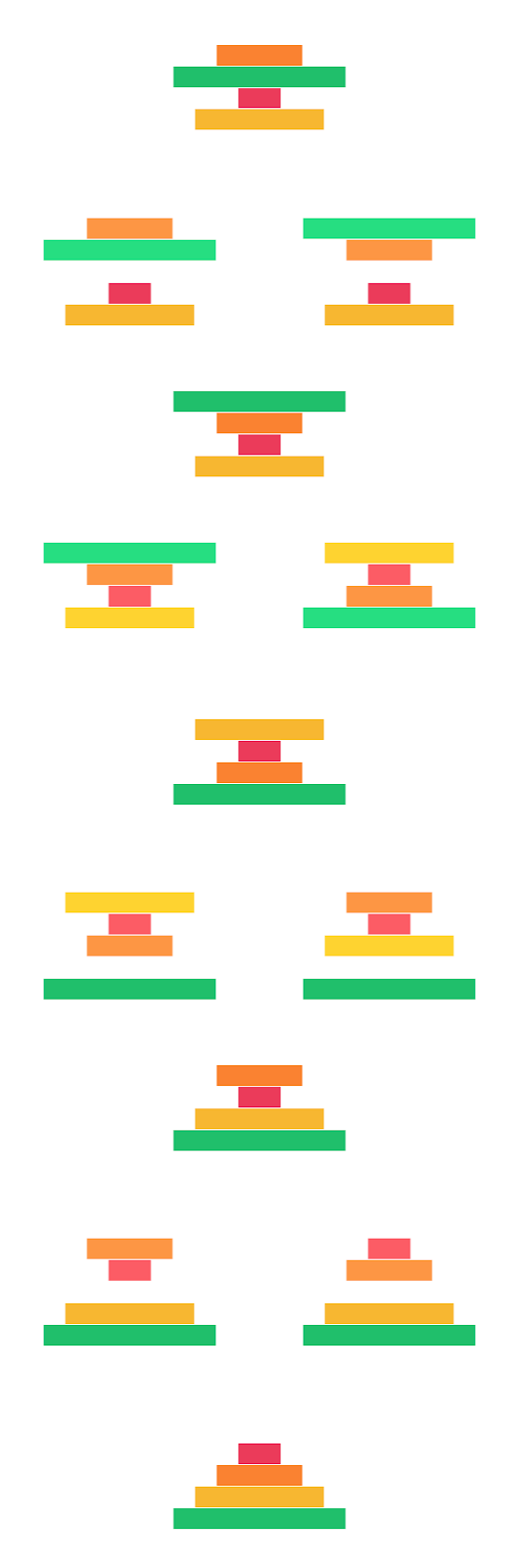
Example

For the stack below, here is a sequence of four flips that orders the pancakes correctly:

Challenges

Here is a collection of puzzles. The low floor version of the activity is to find a way to use the spatula operation to get the pancakes in the right order for each puzzle. There are two higher-level asks:

• Find a reliable algorithm for spatula-sorting the stack: Can you find a set of instructions that you could give to a friend so if they follow them, they'll be able to put any stack of pancakes in order?

• Find optimal solutions: For each puzzle, what is the minimum number of flips you need to make to sort the stack?

(Ideally you would find an algorithm that sorts them with a minimum number of flips!)

Notes

• The standard algorithm for inverting a stack of \(n\) pancakes does it in \(2n-3\) flips, at worst. The procedure works as follows:

  At any point where the largest \(k\) pancakes are at the bottom of the stack in the right order, we consider them the lower stack and the remaining \(n-k\) pancakes the upper stack. Find the largest pancake that is in the upper stack -- i.e., in the incorrect position. If it is not at the very top of the stack, place the spatula under it and flip so that it becomes the top pancake. Then flip the entire upper stack so that this pancake lies on top of the bottom stack, putting it in the correct position. The bottom stack now has \(k+1\) pancakes and the bottom has \(n-k-1\). Repeat this procedure until the bottom stack has all \(n\) pancakes.

• It is known that for \(n\) pancakes, the worst case scenario is the stack takes somewhere between \(15n/14\) and \(18n/11\) flips. As \(n\) gets large, \(18n/11\) is much less than \(2n-3\), so the standard algorithm is not particularly efficient (spatula-wise)! It has been shown that the problem of sorting optimally is NP-hard, so an efficient (runtime-wise) algorithm capable of sorting any stack in the least number of flips likely won't be found anytime soon, if one even exists!

  On the other hand, you can come up with inefficient algorithms for doing it that rely on exhaustive search. Given a stack of \(n\) pancakes, you can try each of the \(n-1\) flips that reorder the pancakes. If none of those produce an ordered stack, you can take each of them and apply the \(n-1\) flips to each of those. After \(k\) iterations, you'll have done

  \[ (n-1)^k \]

  operations, where in the worst cases, \(15n/14 \leq k \leq 18n/11\). This is a huge number of calculations to do and a huge number of things to store in memory. You can clean this up by keeping track of things you've seen before, since you should never have to branch off from the same arrangement twice, and there are only \(n!\) possible arrangements of pancakes. (Still computationally huge, but smaller!)

• As of this writing, people have computed the worst case number of flips to sort \(n\) pancakes up through \(n = 19\):

  Pancakes	Flips (worst case)
  \(1\)	\(0\)
  \(2\)	\(1\)
  \(3\)	\(3\)
  \(4\)	\(4\)
  \(5\)	\(5\)
  \(6\)	\(7\)
  \(7\)	\(8\)
  \(8\)	\(9\)
  \(9\)	\(10\)
  \(10\)	\(11\)
  \(11\)	\(13\)
  \(12\)	\(14\)
  \(13\)	\(15\)
  \(14\)	\(16\)
  \(15\)	\(17\)
  \(16\)	\(18\)
  \(17\)	\(19\)
  \(18\)	\(20\)
  \(19\)	\(22\)

  These are called pancake numbers. If \(P(n)\) is the \(n\)th pancake number,

  \[ P(n) \leq P(n+1) \leq P(n)+2 \]

  The idea is as follows: For \(n+1\) pancakes, find the largest one and put it in the bottom position. This takes \(0\) flips if it's there already, \(1\) flip if it's in the top position, and \(2\) flips if it's somewhere in between. Now the \(n\) pancakes on top can be sorted in at most \(P(n)\) flips. (We definitely need at least \(P(n)\) at worst, since the worst case of \(n\) pancakes on top of a largest \((n+1)\)st pancake will take exactly \(P(n)\) flips.)

Extra Challenges

• The traditional challenge is to give the pancakes distinguishable sides -- for example, one side is burnt and the other fluffy. Now when a part of the stack is flipped, the pancakes switch from fluffy-side-up to burnt-side-up and vice versa. How can you sort the stack so that the pancakes are in order and all fluffy-side-up? In particular:

  • What's a good general algorithm for sorting the pancakes?

  • What's the least number flips required for a given stack?

• My colleague Steve Heller suggested a generalization I like a lot: The spatula allows you to take a substack of pancakes from the top and flip it. What if you could also do so from the bottom? In the absence of antigravity pancakes, it seemed a nice way to think about this was a bookshelf with books of different heights. You are allowed to take some number of books from the left or from the right and flip them in place, keeping the spines toward you. The fluffy-burnt generalization could be cast in terms of the titles on the spines needing to be read correctly when you tilt your head to the right.

• Another direction of generalization is to allow some of the pancakes to be the same size. For example, suppose you have a stack of pancakes of sizes \(1,2,3,3,4,4,5\) that must end in that order.

• Finding an arrangement of pancakes that takes a lot of flips is trickier than it looks! Students might like to find an arrangement of \(8\) pancakes that requires \(9\) flips, for example. On the other hand, the sweet spot for interesting puzzles seems to a puzzle that requires fewer flips to solve than one would initially suspect. Students might like to come up with their own arrangements of pancakes that have a short, clever solution and challenge each other to solve them with the smallest number of flips.

This post was sponsored by the Julia Robinson Mathematics Festival